Consideremos nuevamente el
siguiente problema. En consejo de curso se decide comprar
2 destacadores, 5 lápices y 3 cuadernos.
Para determinar el costo de los útiles,
se sabe que 1 destacador más 4 cuadernos más 3 lápices
se valen $ 2600, 2 destacadores más 5 cuadernos más 4 lápices
valen $ 3500 y 1 destacador más 3 cuadernos más 2 lápices
valen $ 2000.
¿Cuál es el costo total de los
útiles?
Para resolver este problema,
vamos a determinar el costo por unidad de cada uno de los
útiles: destacador, cuaderno y lápiz.
De acuerdo a los datos
proporcionados, podemos construir el siguiente sistema de
ecuaciones:
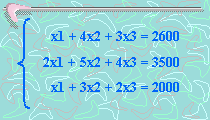
Donde
x1 = Precio de un destacador
x2 = Precio de un cuaderno
x3 = Precio de un lápiz
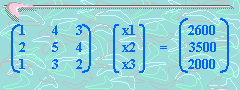
O bien:
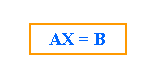
Donde
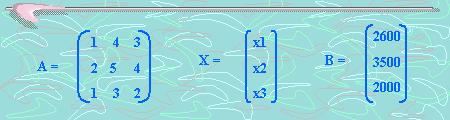
La matriz
A es la matriz de coeficientes, la matriz X es la matriz
de las incógnitas y por último, la matriz B es la
matriz de los términos independientes.
Para
solucionar la ecuación matricial AX=B, vamos a despejar
la incógnita, que en este caso corresponde a la
matriz X.
Lo que nosotros necesitamos es una matriz tal que, al multiplicarla por la matriz A, nos de cómo resultado la matriz identidad. Llamemos a esa matriz la matriz inversa de A y denotémosla como:
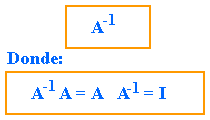
De esta
forma, podríamos resolver nuestra ecuación matricial:
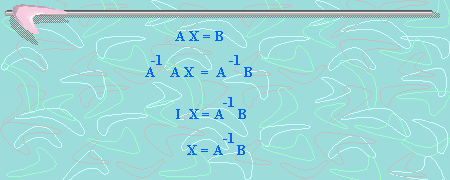
Y solucionado el problema.
Siguiendo
con nuestro problema planteado, tenemos que la matriz
inversa de A es:
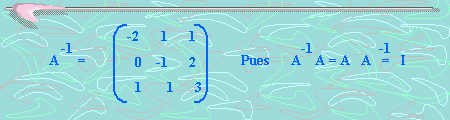
Entonces
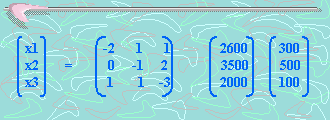
Esto nos
indica que x1= 300, x2= 500 y x3=100. Por lo tanto,
el precio de un destacador, un cuaderno y un lapiz es
respectivamente $300, $500 y $100.
Pero ¿Cómo
se obtuvo la matriz inversa de A?
Como te
puedes dar cuenta, el cálculo de la matriz inversa nos
puede ser muy útil para la resolución de sistemas de
ecuaciones lineales. Ahora, el gran problema se traduce
en como obtenerla.
Es muy
importante que te fijes que el sistema de ecuaciones
anterior tiene la misma cantidad de ecuaciones e
incógnitas,
Ejemplo 1:
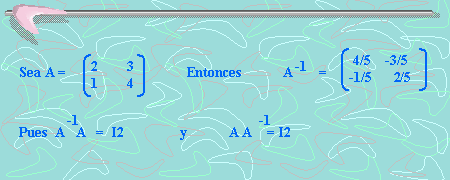
Ejemplo2:
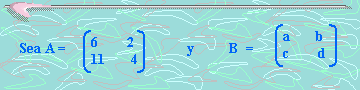
Supongamos que B es la matriz inversa de A. O sea, se tiene que cumplir que:
a)
AB =I2 y
b)
BA =I2
Revisemos a)
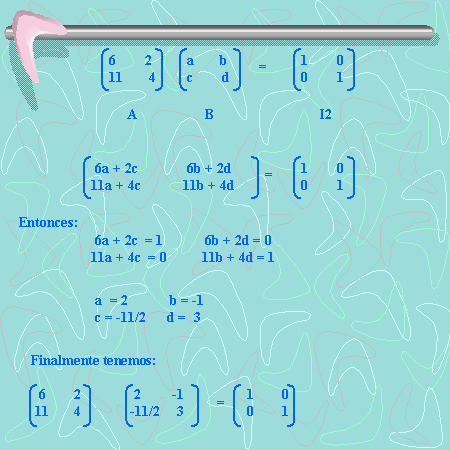
O sea, AB = I2
Revisemos b)
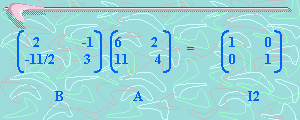
O sea, BA=I2
Por lo tanto,

Ahora,
nuestro principal problema se traduce en obtener la
inversa de una matriz cuadrada, si es que realmente
existe una.
Antes de lanzarnos en esta búsqueda, consideremos las siguientes propiedades respecto a la matriz inversa:
PROPIEDADES DE LA MATRIZ INVERSA
1. Si A y B son matrices cuadradas del mismo orden, ambas inversibles, entonces:
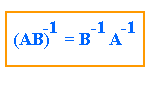
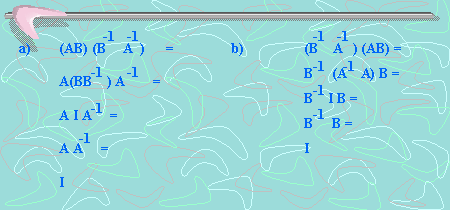
Demostremos esta propiedad:
2. Si la matriz A tiene inversa, esta es única.
3. No toda matriz tiene inversa.
En efecto:
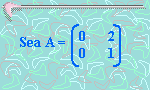
La cual no tiene inversa ya que la siguiente ecuación matricial no tiene solución.
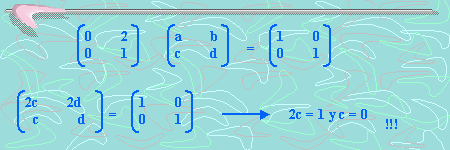
Tenemos que 2c =1 y c=0. En los números reales no podemos tener estas igualdades simultáneamente.
Ahora que ya conoces estas tres propiedades de la matriz inversa, vamos a conocer una matriz especial que nos va a ayudar a encontrar la inversa de una matriz cuadrada. Esta es la matriz adjunta.
Dada una matriz A, el cofactor del elemento aij de la matriz es:
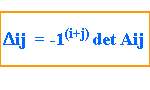
Donde Aij es una submatriz de A obtenida extrayendo la i-ésima fila y la j-ésima columna. Con estos elementos podemos formar una nueva matriz de cofactores de A. denotada como cof(A).
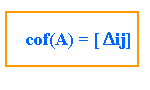
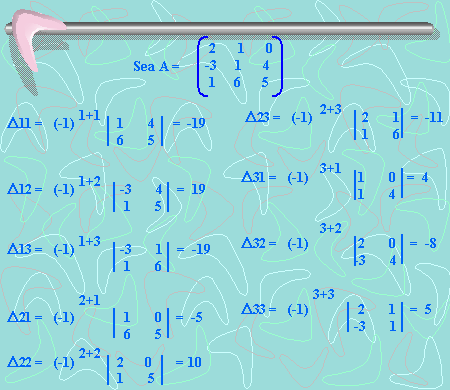
Ejemplo:
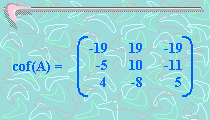
Entonces
Así, dada una matriz cuadrada A, llamaremos matriz adjunta de A a la traspuesta de la matriz de cofactores de A.
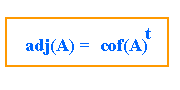
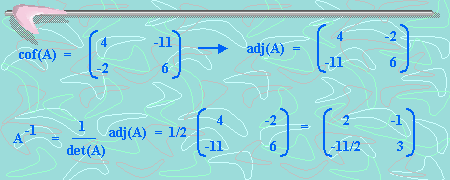
De acuerdo al ejemplo anterior, tenemos:
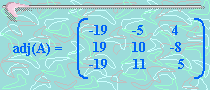
Veamos que pasa si multiplicamos A con adj(A)
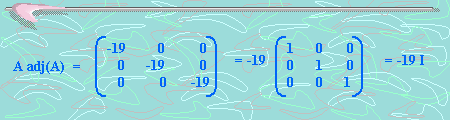
Si calculamos el determinante de la matriz A llegaremos a que det (A) = -19. Luego, en este caso tenemos que:
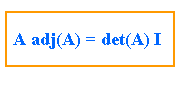
Vamos a suponer esta propiedad válida para toda matriz cuadrada de orden n.
Supongamos ahora que A(nxn) tiene inversa. Usando una de las propiedades de los determinantes tenemos:
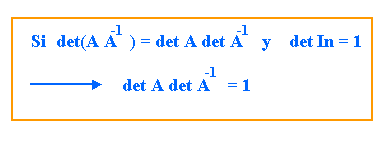
Del producto anterior podemos concluir que si A tiene inversa:
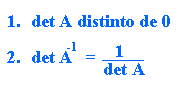
O sea, det A distinto de cero, es una condición necesaria para que A tenga una inversa. Verifiquemos que también es suficiente (o sea, que si el determinante de una matriz es distinto de cero, entonces la matriz es inversible).
Ya sabemos que:

Ahora si que podemos afirmar que:

En este caso:
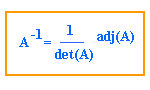
Este resultado nos ofrece un nuevo método para calcular la inversa de una matriz.
Ejemplo 1:
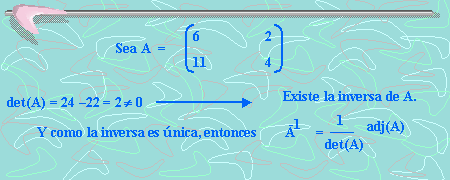
Calculemos la inversa:
Ejemplo2:



