EJERCICIOS MATRIZ INVERSA

1. Dadas las siguientes
matrices:
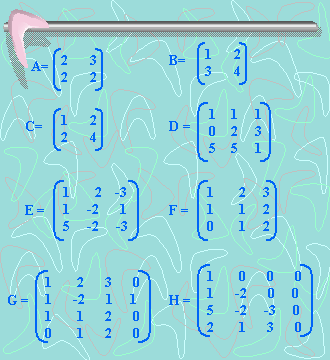
a) ¿Cuál de las siguientes matrices es
invertible?
A B C D E F G H
b) Si la matriz A es
invertible, determinar
su inversa:
c) Si la matriz B es
invertible, determinar
su inversa:
d) Si la matriz C es
invertible, determinar
su inversa:
e) Si la matriz D es
invertible, determinar
su inversa:
f) Si la matriz E es
invertible, determinar
su inversa:
g) Si la matriz F es
invertible, determinar
su inversa:
h) Si la matriz G es
invertible, determinar
su inversa:
i) Si la matriz H es
invertible, determinar
su inversa:
2. Para cada una de las
matrices del ejercicio anterior:
a) Si la matriz es invertible,
determina la inversa de la inversa de la matriz.
b) Determina la inversa de la
matriz traspuesta.
c) Determina la matriz
traspuesta de la inversa de la matriz.
d) Determina la inversa de AB.
Luego multiplica la inversa de B por la inversa de A.
e) Determina la inversa de DF.
Luego multiplica la inversa de F por la inversa de D.
f) De acuerdo a
los ejercicios anteriores (a-e) ¿Cuál(es) de las
siguientes propiedades de las matrices es siempre
verdadera?
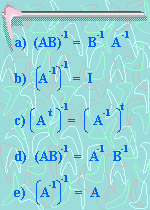
a)
b)
c)
d)
e)
3. Solucionar:
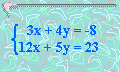
x =
y =
4 Solucionar:
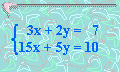
x =
y =
5. Solucionar:
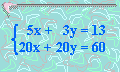
x =
y =
6. Solucionar:
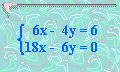
x =
y =
7. Solucionar:
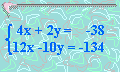
x size="5" name="txt_ej7a" |
y =
8. Solucionar:
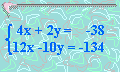
x =
y =
9. Solucionar:
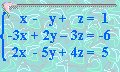
x =
y =
z =
10. Solucionar:
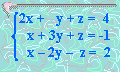
x =
y =
z =
11. Solucionar:
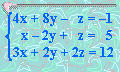
x =
y =
z =
12. Solucionar:
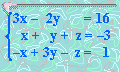
x =
y =
z =
13. Solucionar:
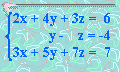
x =
y =
z =
14. Solucionar:

x =
y =
z =
w =
15. La siguiente información
corresponde a la cantidad de energía (calorías) y
proteínas que aportan a nuestro organismo una porción
de leche en polvo con una porción de alimento
fortificante.
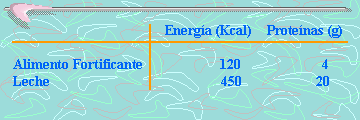
¿Cuántas porciones de leche
en polvo y alimento fortificante se requiere para
ingerir 1800 calorías y 70 gramos de proteínas?
Porciones de
leche Porciones de
alimento
16. Sean 3 números tal
que cuatro veces el primero, más el triple del
segundo, más el triple del tercero es 19.
Veinte veces el primer número, más 20 veces
el segundo, más 10 veces el tercero es 90.
Cuatro veces el primer número, más dos veces el
segundo y más 5 veces el tercero es 29 .
Sean x, y, z los tres números
respectivamente, entonces:
x =
y =
z =
