En esta sección se describe un método para encontrar todas las soluciones (si existen) de un sistema de n ecuaciones con m incógnitas.
Imagina
que estás en consejo de curso y ocurre la siguiente
problemática. Se decide comprar 2 destacadores, 5 lápices
y 3 cuadernos. Para determinar el costo de los útiles,
se sabe que el año pasado se gastó en 1 destacador más
4 cuadernos más 3 lápices $ 2600; 2 destacadores más 5
cuadernos más 4 lápices segastó $ 3500 y 1 destacador
más 3 cuadernos más 2 lápices se gastó $ 2000.
Para
resolver este problema, vamos a determinar el costo por
unidad de cada uno de los útiles: destacador, cuaderno y
lápiz.
De
acuerdo a los datos proporcionados, podemos construir el
siguiente sistema de ecuaciones:
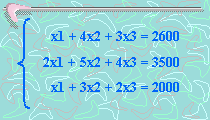
Donde
x1 = Precio de un destacador
x2 = Precio de un cuaderno
x3 = Precio de un lápiz
Para
comenzar, vamos a enumerar las ecuaciones del sistema de
1 a 3 y vamos a asociar el sistema anterior a la matriz
de coeficientes como sigue:
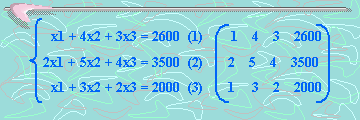
Primer paso: Eliminemos x1 de las ecuaciones (2) y (3). Para esto, multipliquemos la ecuación (1) por –2 y sumemos la ecuación obtenida a la ecuación (2), obteniendo una nueva ecuación (2’).
Multipliquemos la ecuación (1) por –1 y sumémosla a la ecuación (3), obteniendo la ecuación (3’). Esto nos da como resultado el siguiente sistema de ecuaciones:
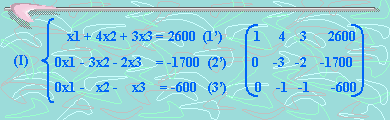
Segundo paso : Eliminemos x2 de la ecuación (1’). Para esto, multipliquemos la ecuación (3’) por 4 y luego sumémosla a la ecuación (1’), obteniendo la ecuación (1’’).
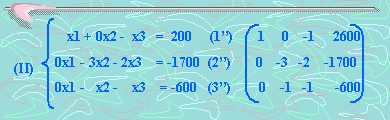
Tercer paso: Multipliquemos la ecuación (3’’) por –3. El sistema queda así:

Cuarto paso:
Eliminemos x2 de la ecuación (3’’’).
Sumemos la ecuación (2’’’) a la ecuación
(3’’’), obteniendo la ecuación (3iv).
El sistema quedaría así:
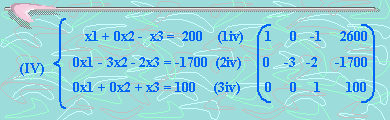
Quinto paso: Eliminemos x3 de la ecuación (1iv) y (2iv). Para esto, sumemos la ecuación (3iv) a la ecuación (1iv), obteniendo la nueva ecuación (1v).
Multipliquemos
la ecuación (3iv) por 2 y luego sumémosla a la ecuación
(2iv), obteniendo la nueva ecuación (2v).
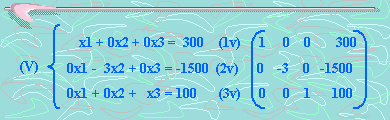
Sexto paso:
Multipliquemos la ecuación (2v) por –1/3,
obteniendo la ecuación (2vi).

O sea:
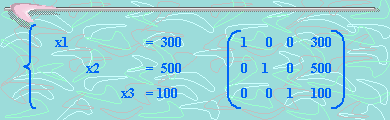
Del sistema anterior, podemos desprender que:
x1 = 300
Esto
quiere decir que el precio de un destacador, un cuaderno
y un lápiz es respectivamente: $100, $500 y $100.
Resolviendo
el problema que teníamos en un comienzo, tenemos que el
costo total de los útiles es $2600. Pues:
Si representamos en forma matricial el sistema del problema anterior tenemos:
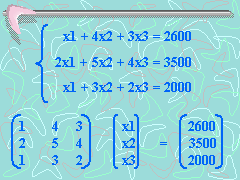
La matriz ampliada asociada al sistema es:

Con todas las operaciones que relizamos llegamos a:

que es la matriz ampliada resultante del sistema:

Ahora, vamos a definir las tres operaciones que anteriormente realizamos.
OPERACIONES ELEMENTALES SOBRE LAS FILAS DE UNA MATRIZ
1. Permutación de la i-ésima y j-ésima fila.
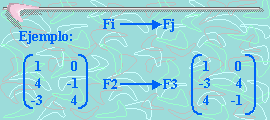
2. Multiplicación de la i-ésima fila por un escalar no nulo k.
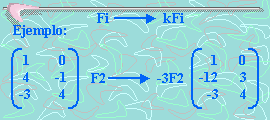
3. Sustitución de la i-ésima fila por la i-ésima fila más k veces la j-ésima fila.
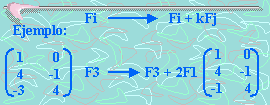
El proceso de aplicar las operaciones elementales con filas para simplificar una matriz aumentada se llama reducción por filas.
Siendo consecuentes con lo anterior, si A y B son matrices de orden nxm, diremos que B es equivalente (por filas) a la matriz A si B fue obtenida de A a través de un número finito de operaciones elementales sobre las filas de A. Esto lo denotaremos como:
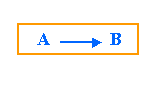
Por ejemplo:

pues

Otro ejemplo
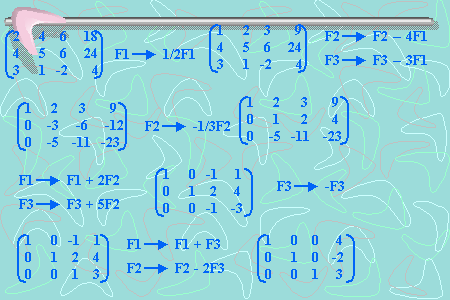
De nuevo se puede "ver" de inmediato que la solución es:
x1 = 4, x2 = -2, x3 = 3
SOLUCIÓN DE UN SISTEMA CON UN NÚMERO INFINITO DE SOLUCIONES
Resolvamos el sistema:

Escribamos el sistema como una matriz ampliada:

Después, se obtiene sucesivamente,
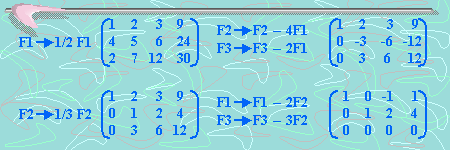
Esto es equivalente al sistema de ecuaciones
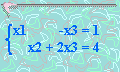
Hasta aquí se puede llegar. Se tienen solo dos ecuaciones para las tres incógnitas x1, x2, x3 y existe un número infinito de soluciones. Para ver esto, se elige un valor de x3. Entonces
x2 = 4 - 2x3
x1 = 1 + x3
Esta será una solución para cualquier número x3. Por ejemplo, si x3 =0 se obtiene x1 = 1 y x2 = 4. Si x3 = 10 se obtiene x1 =11 y x2 = -16.
UN SISTEMA INCONSISTENTE
Resuelve el sistema
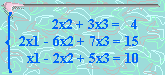
La matriz ampliada para este sistema es

Tratemos de resolver este sistema
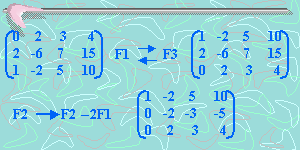
Hagamos una pausa aquí; las últimas dos ecuaciones son
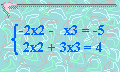
Lo que es imposible, ( si -2x2 - 3x3 = -5, entonces 2x2 + 3x3 =5, no 4 ). así no hay una solución. Se puede proceder de otra forma para obtener una forma más estándar:
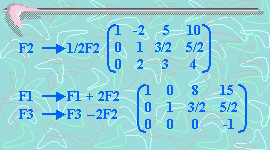
Ahora la última ecuación es 0x1 + 0x2 + 0x3 = -1, lo que es imposible ya que 0 es distinto de -1. Así, el sistema anterior no tiene solución en los reales. En este caso se dice que el sistema es inconsistente.
Luego

FORMAS ESCALONADAS REDUCIDAS POR FILAS
Analicemos estos tres ejemplos vistos anteriormente

Las matrices R1, R2 y R3 se llaman formas escalonadas reducidas por filas de las matrices A1, A2 y A3 respectivamente. En general, tenemos la siguiente definición:

Definamos ahora lo que es un PIVOTE

La condición (iii) anterior, se puede restablecer como "el pivote en cualquier fila está a la derecha del pivote de la fila anterior".
Ejemplo: Las siguientes matrices están en la forma escalonada reducida por filas:

Las matrices (i) y (ii) tienen tres pivotes; las otras tres matrices tienen dos pivotes.

Ejemplo: Las siguientes matrices se encuentran en forma escalonada por filas:

Resolvamos el siguientes sistema de ecuaciones reduciendo la matriz de coeficientes a la forma escalonada por filas.

Comencemos con la matriz ampliada:

Hasta aquí, este proceso es idéntico al anterior; pero ahora solo se hace cero el número (-5) que está abajo del primer 1 en la segunda fila:

La matriz aumentada del sistema (y los coeficientes de la matriz) se encuentran ahora en la forma escalonada por filas y se puede ver de inmediato que x3 = 3.
Después se usa la sustitución hacia atrás para despejar primero x2 y después x1.
El método de solución que se acaba de emplear se llama Eliminación Gaussiana.
Ahora tenemos dos métodos para resolver sistemas de ecuaciones.



