EJERCICIOS GAUSS-JORDAN, ELIMINACIÓN GAUSSIANA

1. ¿Cuál de los siguientes sistemas tiene la matriz de coeficientes dada?

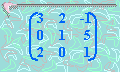
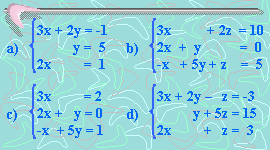
2. ¿Cuál de las siguientes es una operación elemental con filas?

a) Remplazar una fila con un múltiplo diferente de cero de esa fila.

b) Sumar una constante diferente de cero a cada elemento en una fila.

c) Intercambiar dos columnas.

d) Remplazar una fila por una suma de filas y una constante distinta de cero.

3. ¿Cuál de las siguientes afirmaciones es cierta sobre la matriz dada?

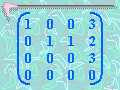
a) Está en la forma escalonada por fila.

b) No está en la forma escalonada por fila porque el cuarto número en la fila 1 no es 1.

c)  No está en la forma escalonada por fila porque el primer elemento diferente de cero en la fila 3 es 3.

d)  No está en la forma escalonada por fila porque la última columna contiene un cero. 

4. ¿Cuál de las siguientes afirmaciones es cierta sobre el sistema dado?

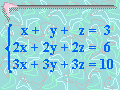
a) Tiene uns solución única x = 1; y = 1; z = 1

b) Es inconsitente.

c) Tiene un número infinito de soluciones.

5. Utiliza la eliminación de Gauss-Jordan para encontrar todas las soluciones (si existen) para los sistemas dados:

a) ¿Cuál(es) sistema(s) tiene(n) una única solución?

a)   b)   c)   d)   e)   f)   g)   h)  i) 

b) ¿Cuál(es) sistema(s) no tiene(n) solución?

a)   b)   c)   d)   e)   f)   g)   h)  i) 

c) ¿Cuál(es) sistema(s) tiene(n) infinitas soluciones?

a)   b)   c)   d)   e)   f)   g)   h)  i)  

6. Dadas las siguiente matrices:

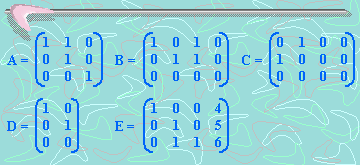
a) ¿Cuál(es) matriz(ces) se encuentra(n) en la forma escalonada por filas, pero no en la forma escalonada reducida por filas?

A   B   C   D   E  

b) ¿Cuál(es) matriz(ces) se encuentra(n) en la forma escalonada reducida por filas?

A   B   C   D   E  

c) ¿Cual(es) matriz(ces) no se encuentra(n) en ninguno de los dos casos anteriores?

A   B   C   D   E  

7. Dadas la siguientes matrices. 

¿Cuál de las siguientes afirmaciones es verdadera?

a) La matriz L es la forma escalonada por filas de la matriz A.

b) La matriz I es la forma escalonada por filas de la matriz C.

c) La matriz E es la forma escalonada reducida por filas de la matriz B.

d) La matriz H es la forma escalonada reducida por filas de la matriz A.

e) La matriz E es la forma escalonada por filas de la matriz B.

f) La matriz K es la forma escalonada reducida por filas de la matriz B.

g) La matriz D es la forma escalonada por filas de la matriz C.

h) La matriz J es la forma escalonada reducida por filas de la matriz C.

i) La matriz F es la forma escalonada por filas de la matriz A.

a)   b)   c)   d)   e)   f)   g)   h)   i) 

8. Solucionar:

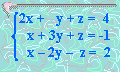
x =      y =      z = 

9. Solucionar:

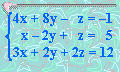
x =      y =      z = 

10. Solucionar:

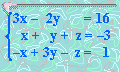
x =      y =      z = 

11. Solucionar:

x =      y =      z =      w = 

12. La siguiente información corresponde a la cantidad de energía (calorías) y proteínas que aportan a nuestro organismo una porción de leche en polvo con una porción de alimento fortificante.

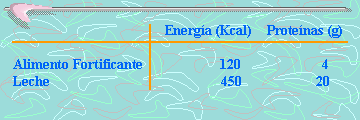
¿Cuántas porciones de leche en polvo y alimento fortificante se requiere para ingerir 1800 calorías y 70 gramos de proteínas?

Porciones de leche      Porciones de alimento 

13.  Sean 3 números tal que cuatro veces el primero, más el triple del segundo,  más el triple del tercero es 19. Veinte veces el primer número,  más 20 veces el segundo,  más 10 veces el tercero es 90. Cuatro veces el primer número, más dos veces el segundo y más 5 veces el tercero es 29 .

Sean x, y, z  los tres números respectivamente, entonces:

x =       y =       z = 

14. Un mueblero fabrica sillas, mesas para café y mesas para comedor. Se necesitan 10 minutos para lijar una silla, 6 para pintarla y 12 para barnizarla. Se necesitan 12 minutos para lijar una mesa para café, ocho para pintarla y 12 para barnizarla. Se necesitan 15 minutos para lijar una mesa para comedor, 12 para pintarla y 18 para barnizarla. La mesa de lijado está disponible 16 horas a la semana, la mesa de pintura 11 horas a la semana y la mesa de barnizado 18 horas ¿Cuántas unidades de cada mueble deben fabricarse por semana de modo que las mesas de trabajo se ocupen todo el tiempo disponible?

15. Un editor publica un posible éxito de librería en tres presentaciones distintas: libro de bolsillo, club de lectores y edición de lujo. Cada libro de bolsillo necesita un minuto para el cosido, dos para el pegado y 3 para el secado. Cada libro para el club de lectores necesita dos minutos para el cosido, cuatro para el pegado y 5 para el secado. Cada libro en edición de lujo necesita tres minutos para el cosido, cinco para el pegado y 7 para el secado. Si la planta de cosido está disponible seis horas diarias, la planta de pegado 11 horas diarias y la planta para secado 15 horas diarias ¿Cuántos libros de cada presentación se pueden producir por día de modo que las plantas se aprovechen a toda su capacidad?

16. Un viajero que acaba de regresar de Europa gastó $30 diarios en Inglaterra, $20 en Francia y $20 diarios en España por concepto de hospedaje. En comida gastó $20 diarios en Inglaterra, $30 diarios en Francia y $20 diarios en España. Sus gastos adicionales fueron  de $10 diarios en cada país. Los registro del viajero indican que gastó un total de $250 en hospedaje, $230 en comida y $200 en gastos adicionales durante su viaje por estos tres países. ¿Cuántos días que pasó el viajero en cada país?