Articulo de: J J O'Connor and E F Robertson

Traducción desde la página:

http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Matrices_and_determinants.html  

Los comienzos de las matrices y los determinantes datan del siglo II AC, aunque hay indicios desde IV siglos AC. Sin embargo, no fue hasta fines del siglo XVII que las ideas reaparecieron y se desarrollaron con fuerza. Los comienzos de las matrices y los determinantes surgen a través del estudio de sistemas de ecuaciones lineales. En Babilonia se estudiaron problemas que involucraban a ecuaciones lineales simultáneas y algunos de estos son conservados en tabletas de arcilla que permanecieron en el tiempo. Por ejemplo, una tableta que data alrededor de 300 años AC contiene el siguiente problema:

"Hay dos terrenos cuya área total es de 1800 metros cuadrados. Uno produce granos en una proporción de 2/3 de una medida por yarda cuadrada mientras el otro produce granos en una proporción de 1/2 de una medida por metro cuadrado. Si la producción total es 1100 medidas, ¿Cuál es el tamaño de cada terreno?"

Los Chinos, entre los años 200 AC y 100 AC, estuvieron mucho más cerca de las matrices que los babilonios. Verdaderamente es justo decir que el texto “Nueve Capítulos de Arte Matemático”, escrito durante la Dinastía Han, da el primer ejemplo conocido sobre métodos matriciales. Por ejemplo, el problema siguiente es muy similar al ejemplo anterior dado en Babilonia:

"Hay tres tipos de cereal, de los cuales tres fardos del primero, dos del segundo, y uno del tercero hacen 39 medidas. Dos del primero, tres del segundo y 1 del tercero hacen 34 medidas. Y uno del primero, dos del segundo y tres del tercero hacen 26 medidas. ¿Cuántas medidas de cereal son contenidas en un fardo de cada tipo?"

Ahora, para resolver este problema, el autor hace algo realmente extraordinario. Coloca los coeficientes del sistema de tres ecuaciones lineales en una especie de  "tablero contador".

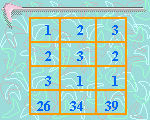
En nuestro siglo XX, escribimos las ecuaciones lineales por medio de filas más que por columnas pero, naturalmente, el método es idéntico. Más extraordinario, es que hace 200 años AC, el autor escribió instrucciones al lector:

1. Multiplicar la columna dos por tres y la columna tres por dos, restar la nueva columna tres a la columna dos, generando una nueva columna dos.  Luego, multiplicar la columna uno por tres y restarle la columna tres generando una nueva columna uno. El tablero contador queda así:

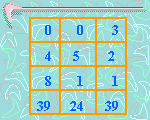
2. Multiplicar la columna uno por cinco y la columna dos por cuatro, restar la nueva columna dos a la columna uno, generando una nueva columna uno. El tablero contador queda así:

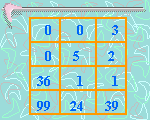
Con esto, tenemos la solución para el tercer tipo de cereal, de este modo se puede  encontrar la solución para el segundo y por último para el primero por medio de la sustitución hacia atrás. Este método, conocido ahora como Eliminación Gaussiana, no se volvería a retomar sino hasta inicios del siglo XIX.

  Cardan, en “Ars Magna” (1545), da una regla para resolver un sistema de dos ecuaciones lineales que llama regla de modo. Resulta que esta regla  corresponde en esencia a nuestra conocida Regla de Cramer  para la resolución de  un sistema de (2 x 2).  Aunque Cardan no daba aún el  paso final,  no alcanzó la definición de determinante pero,  ahora  podemos ver que su método conducía a la definición.

Muchos resultados  estándar de teoría de matrices elementales aparecieron antes de que las matrices fueran objeto de investigación matemática. Por ejemplo, de Witt en “Elementos de curvas”, publicado como una parte de la comentada “Versión Latina de la Geometría de Descartes”  en 1660, muestra como una transformación de ejes reducen una ecuación dada de una cónica a la forma canónica. Esto resultaba de la diagonalización de una matriz simétrica  pero, de Witt nunca pensó en estos términos.

La idea de determinante apareció en Japón y Europa casi al mismo tiempo, aunque Seki en Japón ciertamente lo publicó primero. En 1683, Seki escribía “Métodos de  Resolución de problemas Disimulados”  que contienen métodos  matriciales escritos exactamente como en las tablas del método chino descrito anteriormente. Sin tener alguna palabra que correspondiera a 'determinante', Seki  los introdujo y dio métodos generales para calcularlos basados en ejemplos. Usando sus 'determinantes' Seki fue capaz de encontrar determinantes en matrices de orden (2 x 2), (3 x 3), (4 x 4) y (5 x 5)  y los aplicó para resolver ecuaciones pero, no sistemas de ecuaciones lineales. Más extraordinario aún, es que la aparición del primer determinante en Europa coincidía con el mismo año 1683. En ese año Leibniz escribía  a de l'Hôpital.

Tenía una solución porque:

Esta es exactamente la condición para que el coeficiente de la matriz tenga determinante cero. Note que Leibniz no estaba usando coeficientes numéricos pero...

"dos caracteres, el primero marcando en que ecuación  ocurre, el segundo marcando a que columna pertenece."

Así,  21 significa lo que nosotros escribimos como a21.

Leibniz estaba convencido de que una buena notación matemática era la llave hacia el progreso, así, experimentó con diferentes  notaciones para sistemas de coeficientes. Sus inéditos manuscritos contienen mas de 50 formas diferentes para escribir sistemas de coeficientes. Trabajó con esto durante un período de 50 años, comenzando en 1678. Solo dos publicaciones (1700 y 1710) contienen resultados sobre sistemas de coeficientes y estos usaron la misma notación como en su nota a de l'Hôpital. mencionada anteriormente.

Leibniz usó la palabra 'resultante' para cierta suma combinatorial de términos de un determinante. Probó resultados diversos en resultantes, incluyendo lo que en esencia corresponde a la Regla de Cramer. El también sabía que un determinante podía ser expandido usando alguna columna, método que es llamado ahora "Expansión de Laplace". Así como estudió sistemas de coeficientes de ecuaciones que lo guiaron a los determinantes, Leibniz también estudió sistemas de coeficientes de formas cuadráticas que lo llevaron, naturalmente, hacia la teoría de matrices.

Por los años 1730, Maclaurin escribió “Tratados de álgebra”  el cual no fue publicado sino hasta 1748, dos años después de su muerte. Este tratado contiene los primeros  resultados publicados sobre determinantes probando la regla de Cramer para sistemas de (2 x 2) y (3 x 3) e indicando como trabajar para sistemas de (4 x 4). Cramer daba la regla general para sistemas de (n x n)  en “Introducción  al análisis de curvas algebraicas”  (1750). Esto surgió motivado por el  deseo de encontrar la ecuación de una curva  plana pasando a través de un número dado de puntos. La regla aparece en un apéndice del documento, pero la prueba no aparece:

"Se encuentra el valor de cada incógnita formando n fracciones de las cuales el común denominador tiene tantos términos como hay permutaciones de n cosas."

Cramer  explica precisamente el cálculo de estos términos como el producto de ciertos coeficientes en las ecuaciones y como se  puede determinar el signo. El también explica como los n numeradores de las fracciones pueden ser encontrados reemplazando ciertos coeficientes en este cálculo por términos constantes del sistema.

Los trabajos sobre determinantes  empezaban a aparecer con regularidad. En 1764 Bezout daba métodos para calcular determinantes como lo hacia Vandermonde en 1771. En 1772, Laplace afirma que los métodos introducidos por Cramer y Bezout eran impracticables y, en un escrito donde él estudiaba las órbitas de planetas, discutía la solución de sistemas de ecuaciones lineales sin  calcularlos pero, usando determinantes. Más sorprendente aún, Laplace usaba la palabra 'resultante’  para denotar determinantes. Es más sorprendente que Laplace usara la misma palabra que Leibniz, más aún, teniendo presente que Laplace no conocía  el trabajo de Leibniz. Laplace daba la expansión de un  determinante como  se conoce actualmente y por ello lleva su nombre.

Lagrange, en un escrito de 1773, estudia la identidad para determinantes de (3x3). Sin embargo, este comentario es hecho en restrospectiva a partir de que Lagrange mismo no vio ninguna conexión entre su trabajo y el de Laplace y Vandermonde. Sin embargo, este escrito de 1773 sobre mecánica,  contiene por primera vez lo que nosotros conocemos ahora como la interpretación del volumen de un determinante. Lagrange mostró que el tetraedro formado por O(0,0,0) y los  tres puntos:

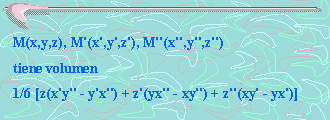
El término 'determinante' fue introducido por primera vez  por Gauss en “Disquisiciones Aritméticas” (1801) mientras se discutían formas cuadráticas. Gauss usó este término porque el determinante determina las propiedades de la forma cuadrática. Sin embargo, este concepto de determinante no era el mismo que conocemos ahora. En el mismo trabajo, Gauss pone los coeficientes de sus formas cuadráticas en arreglos rectangulares. Describe la multiplicación de matrices (la cual piensa como una composición, lo que implica que no había alcanzado aun el concepto de álgebra de matrices) y la inversa de una matriz en el contexto particular de los arreglos de coeficientes de formas cuadráticas.

La Eliminación Gaussiana, que primero aparece  en el texto” Nueve Capítulos de Arte Matemático” escrito 200 años AC, era usada por Gauss en sus estudios de la órbita del asteroide Pallas. Usando las observaciones de Pallas tomadas entre 1803 y 1809, Gauss obtuvo un sistema de seis ecuaciones lineales con seis incógnitas. Gauss ideó un método sistemático para resolver tales ecuaciones, el que precisamente conocemos ahora como “Eliminación Gaussiana”  con  los coeficientes de una matriz.

Fue Cauchy en 1812 quien usó el término 'determinante' en el sentido moderno. El trabajo de Cauchy es el  más completo de los primeros trabajos sobre determinantes. Él desaprobaba los primeros resultados y daba nuevos resultados propios sobre menores. En este escrito, de 1812, por primera vez fue probada la multiplicación de determinantes aunque, en la misma reunión del Instituto de Francia, Binet lee un escrito que contenía la prueba del teorema de la multiplicación pero que fue menos satisfactoria que la realizada por Cauchy.

En 1826 Cauchy, en el contexto de formas cuadráticas en n variables, usó el término 'tableau' para la matriz de coeficientes. Él encuentra el autovalores de matrices y dio resultados sobre diagonalización de una matriz en el contexto de convertir una  forma cuadrática a la suma de cuadrados. Cauchy también introdujo la idea de matrices similares (pero no el término) y mostró que si dos matrices son similares ellas tienen la misma ecuación característica. También probó, nuevamente en el contexto de formas cuadráticas,  que toda matriz simétrica real es diagonalizable.

Jacques Sturm dio una generalización del problema de los autovalores en el contexto de resolver sistemas de ecuaciones diferenciales ordinarias. De hecho, el concepto de autovalores apareció 80 años antes en trabajos sobre sistemas de ecuaciones diferenciales lineales, hechos por D'Alembert  acerca de la generalización del movimiento de una cuerda con masas pegadas a él en diversos puntos.

Es una pena que ni Cauchy ni Jacques Sturm realizaron la generalidad de las ideas que ellos estaba introduciendo, las mostraron solo en los contextos específicos en que ellos estaban trabajando. Jacobi, alrededor 1830 y luego Kronecker y Weierstrass en los años 1850 y 1860 también miraron resultados matriciales pero otra vez en un contexto especial, esta vez relativo a  la idea de un transformación lineal.

Jacobi publicó tres tratados sobre determinantes en 1841. Esto fue de gran importancia, ya que por primera vez la definición de determinante fue hecha en forma  algorítmica y las entradas en los determinantes no fueron especificados. Así, sus resultados fueron aplicados igualmente bien a casos donde las entradas eran números o eunciones. Estos tres escritos de Jacobi hicieron la idea de determinante ampliamente conocido.

Cayley,  también publicó en 1841, la primera contribución Inglesa a la teoría de determinantes. En este escrito, uso dos líneas verticales en ambos lados del arreglo para denotar el determinante, una notación que ahora es común.

Eisenstein en 1844 denotó las sustituciones lineales con  una simple letra y mostró como sumarlas y multiplicarlas como números ordinarios excepto porque no hay commutatividad. Es justo decir que Eisenstein fue el primero en pensar las sustituciones lineales como la formación de un álgebra como pueder ser visto en la siguiente cita de su escrito de 1844:

"Un algoritmo para cálculo puede ser basado en esto,  consiste en aplicar las reglas normales para las operaciones de multiplicación, división y exponenciación a ecuaciones simbólicas. Entre sistemas lineales, ecuaciones simbólicas correctas son obtenidas siempre, teniendo en consideración que el orden de los factores no puede ser alterado."

El primero en usar el término "matriz" fue Sylvester en 1850. Sylvester definió matriz como un arreglo rectangular de términos y vio como algunas matrices contenían dentro de ellas varios determinantes representados como arreglos cuadrados. Después de dejar América, Sylvester volvió a Inglaterra en 1851, y se formó como abogado. Más tarde junto a Cayley, un abogado como él, compartió sus intereses matemáticos. Cayley rápidamente vio el significado del concepto de matriz  y en 1853 había publicado una nota dando, por primera vez, la inversa de una matriz.

Cayley, en 1858,  publicó “Memorias sobre la teoría de matrices”  que contiene  la primera definición abstracta de matriz. Él muestra que los arreglos de coeficiente estudiados tempranamente para formas cuadráticas y para transformaciones lineales son casos especiales de su concepto general. Cayley daba una definición algebraica sobre adición de matrices, multiplicación, multiplicación por un escalar y matriz  inversa. Él daba una construcción explícita de la inversa de una matriz en términos del determinante. Cayley también probó que, en el caso de matrices de orden (2 x 2), la  matriz satisface su ecuación característica propia. Él declaraba que había comprobado el resultado para matrices de orden (3 x 3), indicando su prueba, pero dice:

"Yo no tengo la condición necesaria para llevar adelante el trabajo de probar formalmente el teorema para el caso general de una matriz de cualquier grado."

Que una matriz satisfaga su ecuación característica propia es lo que se conoce como el "Teorema de Cayley-Hamilton". Es razonable preguntarse que tiene que ver esto con Hamilton. En efecto, el también probó un caso especial del teorema, para  matrices de orden (4 x 4), en el curso de sus investigaciones sobre cuaterniones.

En 1870, la forma canónica de Jordan aparece en “ Tratado sobre sustituciones y ecuaciones algebraicas”  por Jordan. Aparece en el contexto de una  forma canónica para sustituciones lineales sobre un campo finito de orden primo.

Frobenius, en 1878, escribió un importante trabajo sobre  matrices en “Sustituciones lineales y formas bilineales” cuando el no estaba consciente del trabajo de Cayley. Frobenius trabajaba en su artículo con coeficientes de formas cuadráticas y  no usa el término matriz. Sin embargo probó importantes resultados sobre matrices canónicas como representaciones de clases de equivalencia de matrices. Él menciona a Kronecker (1874)  y Weierstrass  (1868) como casos especiales de sus resultados respectivamente. Frobenius además probó el resultado general de que una matriz satisfaga su ecuación característica. Este escrito de  1878  también contiene la definición del rango de una matriz  el cual  usaba en sus trabajos sobre formas canónicas y la definición de  Matrices Ortogonales.

La nulidad de una matriz cuadrada  fue definida por Sylvester en 1884. Él definía la nulidad de A, n(A), como el mayor i tal que cada de A de orden (n-i+1)  es nula. Sylvester estaba interesado en invariantes de matrices, esto es, propiedades que cumplen algunas matrices y que no son alteradas bajo ciertas transformaciones. Sylvester provó que:

  max(n(A),n(B)) <= n(AB) <= n(A) + n(B).

En 1896, Frobenius conoció las “Memorias sobre la teoria de matrices”  de  Cayley (1858) y despues comenzó a usar el término matriz. A pesar del hecho que Cayley solo había probado el teorema de Cayley-Hamilton para matrices de (2 x 2) y (3 x 3), Frobenius generosamente atribuyó el resultado a Cayley a pesar de haber sido el, el primero en probar el teorema general.

Una definición axiomática de determinante fue usado por Weierstrass en sus clases y, despues de fallecido,  fue publicado, en 1903, en la nota “Teoría de determinantes”. En el mismo año,  también fueron publicados los apuntes de Kronecker sobre determinantes, nuevamente despues de su muerte. Con estas dos publicaciones, la teoría moderna de determinantes estaba desarrollada pero, la teoría de matrices tomaba un poco más de tiempo para convertirse en una  teoría completamente aceptada.

Un importante texto que abre un espacio para las matrices dentro de las matemáticas fue “Introduccion al álgebra lineal”  escrito por Bôcher en 1907. Turnbull  y Aitken escribieron textos influyentes en los años 1930  y Mirsky con  “Una introducción al álgebra lineal”,  en 1955, mostró laTeoría de Matrices  estableciendola como uno de los más importantes tópicos matemáticos para estudiantes de pregrado.